如何证明三角形内角和为180度
若将三角形的三个内角分别向内折叠,它们会恰好组成一个平角。由于平角的度数为180度,因此,三角形的内角和为180度。用数学符号表示即为:在△ABC中,∠1+∠2+∠3=180°,这也可以表述为全称命题:对于任意三角形△ABC,∠1+∠2+∠3=180°。

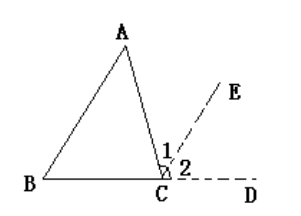
证明方法一:延长BC至点D,并过点C作CE平行于BA。由此可得,∠1与∠A相等,∠2与∠B相等。又因为∠1+∠2+∠ACB的总和等于180°,所以∠A+∠B+∠ACB的总和也等于180°。
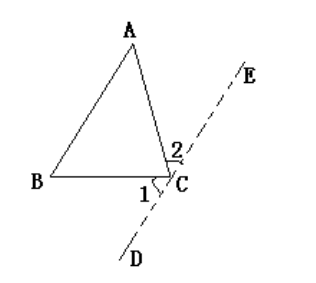
证明方法二:过点C作DE平行于AB。由此可得,∠1与∠B相等,∠2与∠A相等。由于∠1+∠ACB+∠2的总和等于180°,因此∠A+∠ACB+∠B的总和也等于180°。
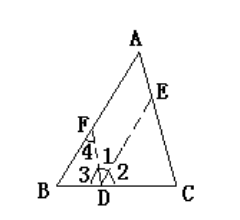
证明方法三:在BC上任意选择一点D,作DE平行于BA并与AC相交于点E,同时作DF平行于CA并与AB相交于点F。由此可得,∠2与∠B相等,∠3与∠C相等,∠1与∠4相等,且∠4与∠A相等。因此,∠1与∠A也相等。又因为∠1+∠2+∠3的总和等于180°,所以∠A+∠B+∠C的总和也等于180°。