直击高考第二天 护考场面暖心
9时,考试铃声响起,高考第二天的考试正式开始。但陪考团在考点外警戒线旁仍然不愿离去,有的家长打开小马扎,就地而坐。大部分家长都沉默地看手机,偶尔有家长互相交流几句,话题也离不开高考和孩子。

直击高考第二天
6月8日,高考进入第二天,考生们怀揣着对未来的憧憬,奔赴考场迎接历史 / 物理、英语科目的挑战。在这场关乎青春与梦想的 “战役” 背后,是一座城市的温暖守护 —— 从家人的深情祝福到校园安保的贴心守护,从交警的烈日下坚守到志愿者的爱心传递,每一个身影都在为考生们构筑起坚实的后盾。
一、校门口的守望:无声的陪伴与鼓励
在山东济宁中学考点外,家长林女士的身影格外动人。她一手撑着伞,一手远远地向考场方向挥手,目光中满是牵挂。“孩子住校,早上直接进考场,我就想趁着上班前过来看一眼。” 林女士说,从高考第一场开始,她每天都会早早来到校门口,只为在孩子进考场前见上一面,挥挥手、笑一笑。
二、校园守护:筑牢安全与温情的防线
(一)校警的雨中守护:从校门口到教学楼的温暖接力
清晨七点,济宁考点搭载考生的车辆陆续停靠,值守的校警们立即行动起来 —— 他们一手打伞,一手搀扶着考生,小心翼翼地将学生们送至遮雨的帐篷下。每一个动作都充满了细致与耐心,仿佛在呵护着一个个珍贵的梦想。
(二)老师的加油仪式:锣鼓声中的青春激励
“永不放弃,敢于超越!”“考神附体,势不可挡!” 早上八点整,济宁考点的教学楼前响起了振奋人心的呐喊。统一身穿紫色上衣的老师们分列两队,手中的标语牌传递着满满的正能量。他们与走向考场的学生们击掌、拥抱,用最热情的方式为孩子们送上祝福。
三、城市护航:多部门联动的暖心行动
(一)交警雨中坚守:用责任守护 “圆梦路”
山东济宁中学考点外,接考生的车辆络绎不绝,校门口的交通压力陡然增大。然而,在风雨中,一群身着警服的身影始终坚守岗位 —— 他们是济宁交警大队的民警们。
(二)志愿者的爱心接力:从物资保障到暖心护送
在济宁一中考点,一群身穿红色马甲的志愿者成为了一道亮丽的风景线。他们是来自各行各业的志愿者团队,早早来到校门口,为考生提供文具、爱心医疗包、矿泉水、雨伞等物品。“我们希望用实际行动为考生们解决后顾之忧,让他们能全身心投入考试。” 志愿者负责人陈先生表示。
2025高考祝福语有哪些
愿所有高考学子从容应考,奋力一搏,不负青春韶华,金榜题名,旗开得胜!
十年寒窗苦,一朝成名耀,金榜题名日,蟾宫折桂时,愿各位高考学子金榜题名,前程似锦!
祝所有高考学生马到成功,高考顺利,所愿皆如愿,所行皆坦途。
愿你挥毫,书写未来华章;愿你搁笔,岁月静好无忧。
青春无悔,奋斗不息,愿你们在高考的战场上展现出自己的最佳状态,金榜题名,前程无限!
高考加油!用汗水铺就成功之路,用努力铸就辉煌未来!
星光不问赶路人,时光不负有心人。在这场人生的盛宴中,你以勤奋为食,用拼搏作酒,历经风雨,终将迎来彩虹。高考加油,未来可期!
高考之路,虽漫漫但其修远兮。在这场知识的盛宴中,你将踏上人生的重要征程。我们为你加油,为你鼓劲,愿你以梦为马,不负韶华。
这个夏天,愿你的成绩如繁星闪烁,点亮你的未来之路,带着期望,你将勇往直前。
(网络收集)2025年全国二卷数学高考真题文字版
- 2,8,14,16,20平均数为
A.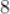
B.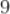
C.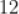
D.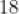
2.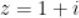 ,
,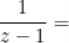
A.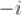
B.
C.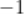
D.
3.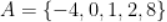 ,
,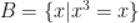 ,
,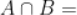
A.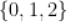
B.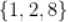
C.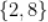
D.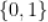
4.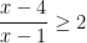 解集是
解集是
A.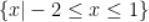
B.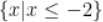
C.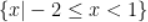
D.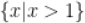
5. 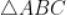 ,
,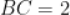 ,
,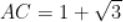 ,
,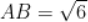 ,
,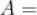
A.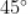
B.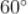
C.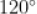
D.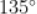
6. 抛物线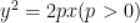 焦点
焦点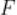 ,
,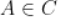 ,过
,过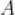 作
作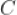 准线的垂线,垂足为
准线的垂线,垂足为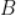 。若
。若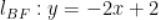 ,则
,则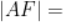
A.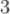
B.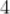
C.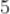
D.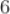
7. 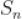 为等差数列
为等差数列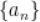 前
前 项和,
项和,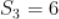 ,
,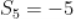 ,
,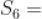
A.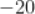
B.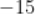
C.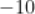
D.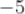
8. 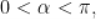 ,
,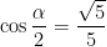 ,
,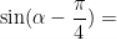
A.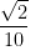
B.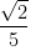
C.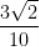
D.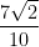
9. 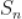 为等比数列
为等比数列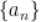 前
前 项和,
项和,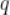 为
为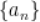 公比
公比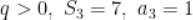 ,则
,则
A.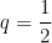
B.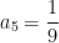
C.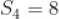
D.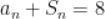
10. 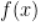 定义在
定义在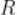 上奇函数,x>0时,
上奇函数,x>0时,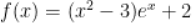 ,则
,则
A.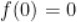
B. 当x<0时,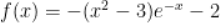
C.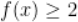 当且仅当
当且仅当
D. 是
是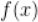 极大值点
极大值点
11. 双曲线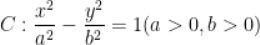 左、右焦点为
左、右焦点为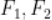 ,左、右顶点为
,左、右顶点为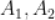 。以
。以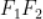 为直径的圆与
为直径的圆与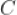 的一条渐近线交于
的一条渐近线交于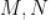 ,且
,且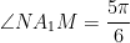 ,则
,则
A.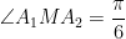
B.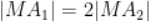
C.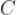 离心率为
离心率为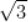
D. 当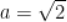 时,四边形
时,四边形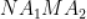 面积为
面积为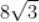
12.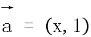 ,
,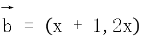 ,
,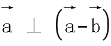 ,则
,则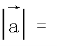 ____
____
13. 是
是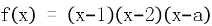 极值点,则
极值点,则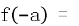 ____
____
14.一个底面半径为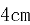 ,高为
,高为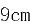 的封闭圆柱形容器,内有两个半径相等的铁球,则铁球半径的最大值为____
的封闭圆柱形容器,内有两个半径相等的铁球,则铁球半径的最大值为____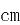 。
。
15.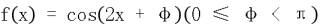 ,
,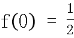
(1) 求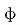 。
。
(2)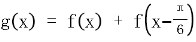 ,求
,求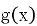 值域和单调区间。
值域和单调区间。
16.椭圆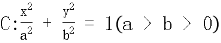 的离心率为
的离心率为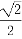 ,长轴长为
,长轴长为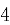 。
。
(1) 求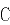 的方程。
的方程。
(2) 过点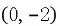 的直线
的直线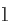 与
与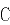 交于
交于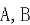 ,
,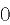 为坐标原点,若
为坐标原点,若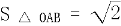 ,求
,求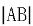 。
。
17.如图,四边形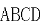 中,
中,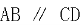 ,
, ,
,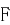 为
为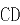 中点,
中点,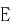 在
在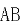 上,
上,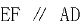 ,
,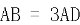 ,
,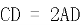 。将四边形
。将四边形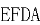 沿
沿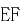 翻折至四边形
翻折至四边形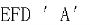 ,使得面
,使得面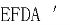 与面
与面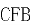 所成的二面角为
所成的二面角为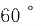 。
。
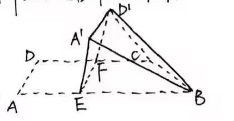
(1) 证明: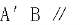 平面
平面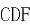 。
。
(2) 求面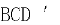 与面
与面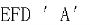 所成二面角的正弦值。
所成二面角的正弦值。
18.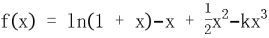 ,
,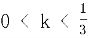 。
。
(1) 证明: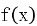 在
在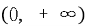 存在唯一极值点和唯一零点。
存在唯一极值点和唯一零点。
(2) 设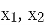 为
为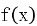 在
在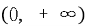 的极值点和零点。
的极值点和零点。
(i)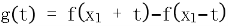 ,证明:
,证明: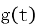 在
在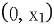 单减
单减
(ii) 比较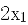 与
与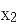 的大小,并证明。
的大小,并证明。
19.甲、乙乒乓球练习,每个球胜者得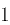 分,负者得
分,负者得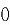 分,设每个球甲胜概率为
分,设每个球甲胜概率为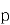 (
(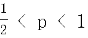 ),乙胜概率为
),乙胜概率为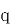 ,
,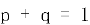 ,且各球胜负独立。对正整数
,且各球胜负独立。对正整数 ,记
,记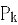 为打完
为打完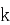 个球后甲比乙至少多得
个球后甲比乙至少多得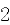 分的概率,
分的概率,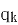 为打完
为打完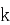 个球后乙比甲至少多得
个球后乙比甲至少多得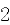 分的概率。
分的概率。
(1) 求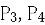 (用
(用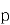 表示)。
表示)。
(2) 若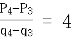 ,求
,求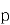 。
。
(3) 证明:对任意正整数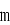 ,
,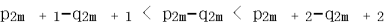 。(2)求面
。(2)求面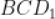 与面
与面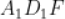 所成二面角的正弦值.
所成二面角的正弦值.







